Small-signal model
Small-signal modeling is a common analysis technique in electrical engineering which is used to approximate the behavior of nonlinear devices with linear equations. This linearization is formed about the DC bias point of the device (that is, the voltage/current levels present when no signal is applied), and can be accurate for small excursions about this point.
Contents |
Motivation
Many electronic circuits, such as radio receivers, communications, and signal processing circuits, generally carry small time-varying signals on top of a constant bias. This suggests using a method akin to approximation by finite difference method to analyze relatively small perturbations about the bias point.
Any nonlinear device which can be described quantitatively using a formula can then be 'linearized' about a bias point by taking partial derivatives of the formula with respect to all governing variables. These partial derivatives can be associated with physical quantities (such as capacitance, resistance and inductance), and a circuit diagram relating them can be formulated. Small-signal models exist for electron tubes, diodes, field-effect transistors (FET) and bipolar transistors, notably the hybrid-pi model and various two-port network
Variable notation
- Large-signal DC quantities are denoted by uppercase letters with uppercase subscripts. For example, the DC input bias voltage of a transistor would be denoted
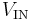 .
.
- Small-signal quantities are denoted using lowercase letters with lowercase subscripts. For example, the input signal of a transistor would be denoted as
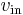 .
.
- Total quantities, combining both small-signal and large-signal quantities, are denoted using lower case letters and uppercase subscripts. For example, the total input voltage to the aforementioned transistor would be
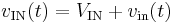 .
.
Example: PN junction diodes
The (large-signal) Shockley equation for a diode can be linearized about the bias point or quiescent point (sometimes called Q-point) to find the small-signal conductance, capacitance and resistance of the diode. This procedure is described in more detail under diode modeling, which provides an example of the linearization procedure followed in all small-signal models of semiconductor devices.
Differences between Small Signal and Large Signal
A small signal model takes a circuit and based on an operating point (bias) it linearizes all the components. Nothing changes because the assumption is that the signal is so small that the operating point (gain, capacitance etc) doesn't change.
A large signal model on the other hand takes into account the fact that the large signal actually affects the operating point and takes into account that elements are non-linear and that circuits can be limited by power supply values. A small signal model ignores supply values.
See also
- Diode modelling
- Hybrid-pi model
- Early effect
- SPICE - Simulation Program with Integrated Circuit Emphasis, a general purpose analog electronic circuit simulator capable of solving small signal models.